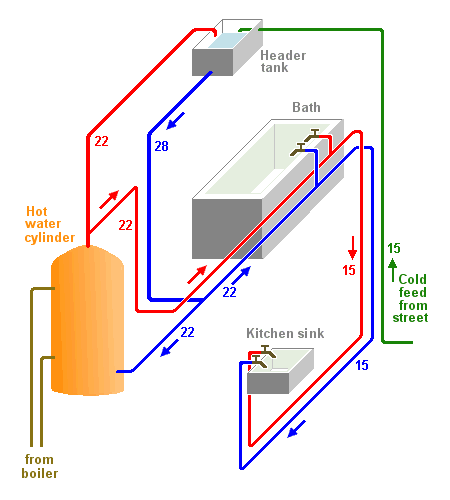
These pages explain how to choose the correct sizes of pipe when plumbing a house, and why it matters. This section explores the theory, and a practical worked example is given in part 2 .
Why do plumbers use so much half-inch copper pipe? This article explains why water pipes in houses are the sizes they are. It shows how to choose the correct size of pipe, why it matters, and whether or not a house water-supply system will work properly once it's installed.
Plumbing books say what to do, but not why. Building services design books offer design rules, but not where they came from nor why they matter, and fluid mechanics textbooks are full of complicated theory that doesn't seem relevant to real problems - Why does this pipe make a noise? - Can I add another radiator?
So I started from first principles, asking basic questions and following up the answers until I could see what was going on. It turned out to be rather more complicated than I thought. Calculations for a real house are in part 2.
Why does water flow?
This question seems almost too stupid to be worth asking, yet it leads to a way of heating the hot-water cylinder without needing a pump.
A pint of water weighs a pound and a quarter...
When you turn on the tap, you expect water to flow out of the tank and down the pipe. Why does it do that?
Things don't just start moving by themselves. There must be a force acting on the water in the pipe for it to move, and the obvious one is its own weight. Water is quite heavy stuff - a litre of it weighs a kilogram. The water in the tank pushes down on the water in the pipe.
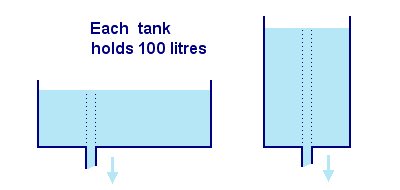
So does the size of the tank matter? Common sense suggests that a big tank that holds more water must apply more force to the water in the pipe than a little one would. But common sense is wrong. The force pushing the water down the pipe has nothing to do with the volume of the tank, nor its surface area.
The force making the water flow down the pipe must exist at the entrance to the pipe. How big is this force? What controls it?
Suppose the water is stationary - any taps connected to the pipe are turned off. Now think about the column of water directly above the pipe entrance (shown as a dotted line). It has weight, and its weight is a force acting downwards. So,
Down-force on the water in the pipe = Weight of water in the column above the pipe
But surely the weight of the water just outside the column affects the down-force too? No, it doesn't. How can it? Weight acts downwards, not sideways. The force due to the weight of the water outside the column acts downwards too - but outside the column. So the down-force in the column stays the same no matter how much water there is around it.
In the sketch above, both tanks hold the same amount of water, but one is twice as tall as the other. The water surface in the taller tank is twice as far away from the pipe, so there is twice as much force pushing water out. If you punctured both tanks near the bottom, water would squirt out much faster from the tall one.
What about the down-force at some point further down inside the pipe? Since the down-force at any point is due solely to the weight of water above it, this force must be bigger at a point further below the water surface, because the column of water above it is bigger and heavier
Suppose the pipe runs vertically, then horizontally under a floor, then down vertically again. The water in the horizontal section has weight too - won't this add to the down-force? Well, no, it won't, for the same reason as before - weight acts downwards on that section of pipe, not sideways. So it turns out that the force that makes the water flow has nothing to do with the size of the tank, nor with the length or shape of the pipe run. It's purely to do with the vertical distance between the water surface in the header tank and the point where the water leaves the pipe at the tap. This distance is known as the head of water for the system.
Water squirts out of a hole
The force acts on the water in the pipe, and the pipe diameter is known, so it's often convenient to think of the force as a pressure. Pressure is simply force divided by area - in this case, the cross-sectional area of the pipe.
Think of a particle of water somewhere in the header tank. With no water moving, the particle is stationary. There is no net force acting on it. If there were, it would move. But there is a force applied to it - the weight of the water above it. And if the particle happened to be near the wall of the tank, and you poked a hole in the tank wall, the particle would escape through it. So there must also be a sideways force from all the particles next to it, or it wouldn't move sideways out of the hole. Yet if it's not moving, all these forces must be in balance. In fact, in a stationary liquid, the pressure at a point is a force that acts in all directions at once: up, down and sideways. The particle is ready to move in any direction at a moment's notice, like the SAS. It's possible, and normal, to talk about the pressure at a point in a liquid.
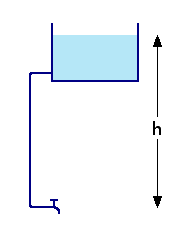
The pressure at the bottom of a vertical pipe is ...
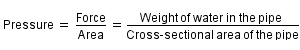
The weight depends on the volume of water (in m3) and its density (in kg/m3). The density of water is about 1,000 kg/m3 - a litre weighs a kilogram. So
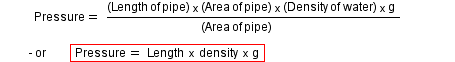
where g is the acceleration due to gravity - about 9.8 m/sec/sec. (Kilograms are about mass, not force, so g has to be included to do the conversion.)
The pressure depends on the length of vertical pipe. In fact, the length that matters is the height difference between the bottom of the pipe and the water surface at the top - in the diagram on the left, the height h. This is known as the head. It's measured in metres, or feet of water, or mm of mercury, or pounds per square inch (psi), or Newtons per square metre (N/sq.m). Whatever units are used, it's still a pressure.
What's a Newton?
 This might be a good point to talk briefly about units. I'm used to thinking in proper engineering units like Newtons and watts, not pounds and BTUs, whatever they may be. British Thermal Underpants?
This might be a good point to talk briefly about units. I'm used to thinking in proper engineering units like Newtons and watts, not pounds and BTUs, whatever they may be. British Thermal Underpants?
Isaac Newton was one of the first to say clearly that
Force = mass x acceleration
The down-force on your hand when you're holding an apple is the mass of the apple (0.1 kg, say) times the acceleration due to gravity (about 10 m/sec/sec). This force is (0.1 kg x 10 m/sec/sec) = 1 Newton. Force these days is measured in Newtons. A Newton is the weight of a small apple - but then, in Newton's time the apples were smaller.
Proper forces, like the weight you can lift with one hand, are lots of Newtons. A bucket holds 9 litres of water (2 gallons) and weighs 8 kg (18 lb.). This weight is a force of 80 Newtons. The pressure on the bottom of the bucket is about 3,000 Newtons per square metre (N/sq.m), though the pressure on your fingers when you're carrying the bucket by its handle is much higher - maybe 50,000 N/sq.m, or 7 psi (lb/sq.in).
Example - 15mm pipe
What force, and what pressure, is exerted by a 1 metre vertical column of water in a 15mm pipe?
A vertical 15mm pipe 1 metre long holds about 0.15 litres of water, which weighs 0.15 kg, giving a down-force on the bottom end of
Force = mass x acceleration = 0.15 (kg) x 9.8 (m/sec/sec) ≈ 1.5 N (Newtons).
This force exerts a pressure of
Pressure = force / area = 1.5 (N) / 145 (sq.mm) = 1.5 x (1,000/0.145) ≈ 10,000 N/sq.m
at the end of the pipe. This sounds huge but actually it isn't very big at all. You could poke your finger in the bottom of the pipe to prevent the water flowing out.
By the way, normal atmospheric pressure is ten times greater than this, but we don't notice it because it surrounds us. Atmospheric pressure is the same at both ends of the pipe, so it can't influence the flow. What matters is pressure difference.
Hot water from gravity
There are lots of ways of heating the water in the cylinder, and one of the oldest methods can be the simplest and cheapest. It depends on the apparently odd fact that hot water weighs less than cold water.
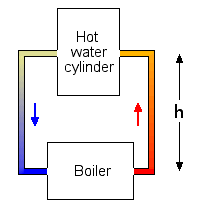 Here is a boiler heating the water in a cylinder. All the boiler does is heat water in the pipe on the right. The water itself does the rest.
To see why, think about the pressures in the pipes on each side of the boiler. The right-hand pipe holds hot water at, say, 82oC. The pressure at the bottom is then:
Here is a boiler heating the water in a cylinder. All the boiler does is heat water in the pipe on the right. The water itself does the rest.
To see why, think about the pressures in the pipes on each side of the boiler. The right-hand pipe holds hot water at, say, 82oC. The pressure at the bottom is then:
Similarly, the pressure at the bottom of the left-hand pipe, which holds water at, say, 65oC, is:
If these two pressures are different, the water will be forced to move. And as the graph shows, water at 82oC is about 1% less dense than the same water at 65oC. This may not sound very much, but it's enough.
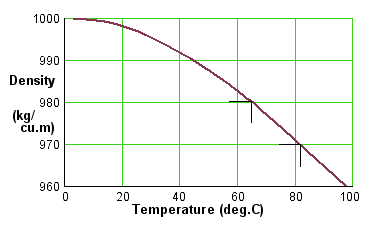
The difference in the density of the water in the flow and return pipes is about 10 kg/m3. A litre of the cold water weighs just 10 grams more than a litre of the hot water. This tiny difference - less than the weight of an English robin - provides the force that makes the water move.
The circulating pressure then seems to be:
![]()
but there is one more detail to factor in.
The water being moved is hot, so it weighs less than cold water, so the circulating pressure would make it move slightly faster than if it were cold water. The correction is easy to add:
It's more usual to express the pressure in a more general way that doesn't directly involve h, because then you can calculate how fast the water will flow round even a complicated circuit. But this is getting ahead of the story. For now, assume that the boiler is on the ground floor and the cylinder is on the floor above, so that h is (say) 3 metres. Then, putting in the numbers for this example, the pressure is
This is a real pressure difference, and the cold water will push the hot water around. The only major drawback is that the pressure difference is so small, which means that the pipes have to be fat for it to work well. But it does work, and it doesn't need a separate pump.
How fast can water flow?
The next obvious question is, what controls the speed of the water that flows out of the tap?
This is where things start getting a little more complicated. Pipes have been in use for quite a long time now, and many clever people have tried to understand exactly what happens when you turn on a tap, but believe it or not, the physics of water flowing in pipes is still more described than explained. The problem lies in friction.
Sticky cylinders
When the water is moving slowly, it's easy. Think of the water in the pipe as a series of thin-walled concentric cylinders, one inside the other, each sliding relative to its neighbours. This is more than just a convenient image. It gives a good picture of what's really going on. The interesting stuff happens where the cylinders rub past each other. The cylinder nearest the pipe wall doesn't really move at all - it seems to be stuck to the pipe. The next one in does move a bit, and as they slide past each other, the outer cylinder exerts a frictional drag on the inner one and slows it down. Similarly, the next one in and the one inside that are slowed down too. The cylinder right in the centre of the pipe moves the fastest.
If you don't believe this, it's possible (but not easy) to set up an experiment to prove it. It does happen.
Some liquids flow more freely than others, and the concept of viscosity was invented to describe the effect. Viscosity is really a definition of how well a liquid resists shear stress - that is, the force making layers of the liquid slide past each other.
Viscosity

Viscosity is measured like this. With a layer of liquid trapped between two parallel plates, the top one is pulled so that it slides steadily over the liquid. The viscosity of the liquid is defined as
The units of viscosity are evidently Newton-seconds per square metre - that is, [Pressure x Time] - though some people prefer "poises" or (my favourite) "feet-slug-seconds". That one really conjures up a picture. But it's useful to have the idea of viscosity, because it says explicitly that a liquid resists being made to move. A force is needed, and the force increases with speed.
Engine oil has a viscosity of about 0.5 N.sec/sq.m., which means that plates 1 metre square separated by an oil film 1mm thick could be slid slowly apart at 1 metre/sec by a strong man applying a force of 500 N (Newtons) - about 100 lb, or 50 kg. A millimetre of cold water, by contrast, needs a force of only 1 N - just a few ounces. A strong Newt could do it, if the Slugs didn't get under its Feet.
If the viscosity of water is so low, why does it matter?
Think back to turning on the tap. As the water in the vertical pipe begins to move, the cylinders of water slide reluctantly past each other. The viscous drag appears as a force acting upwards, opposing the down-force due to the weight of water. The water accelerates, and since the opposing force depends on speed, this viscous drag increases too. Eventually, when the tap is running freely, the forces exactly balance - there is just enough down-force to overcome the friction force at this speed of flow. Viscous friction is the force that controls how fast the water flows. Viscosity explains why the water leaving the tap doesn't just carry on accelerating without limit, as it would if there were no opposing force.
Now, the force pushing downwards is the pressure. More exactly, the net down-force on the water in a length of pipe is the pressure difference between its ends. This down-force is exactly balanced by the opposing up-force due to viscosity. So there must be a simple relationship between the pressure drop in a pipe and the corresponding flow rate. It's not all that difficult to derive it from first principles, if you enjoy integration (and I know some people do). But if you don't feel like doing that right now, the answer is
where μ is the viscosity of the fluid flowing in a pipe of radius R and length L. Unfortunately, although this equation is nice and simple, it comes with a warning - it's only true for slow-moving fluid. But how slow is slow?
Chaos rules
About 120 years ago, in Manchester, a man called Osborne Reynolds was trying to understand - or at least describe - the flow of fluids in pipes. After many careful experiments, he decided that what happened to the flow depended on four things - the viscosity and density of the fluid, the diameter of the pipe, and the speed the fluid was moving. He put these four quantities together like this to make a dimensionless number:
Reynolds number
Speed x Diameter x (Density / Viscosity)
The number has been known ever since as the Reynolds number, Re. Respect!
Reynolds found that when the fluid moves slowly, the flow stays smooth and even, but as the speed is increased it eventually becomes rough and turbulent - chaotic, we would say now. The transition to turbulence always happens at a Reynolds number between 2,000 and 3,000, no matter what fluid is used. (The reason for the uncertainty is probably to do with small variations in initial conditions - chaos is like that.)
In other words, the simple equation above relating flow rate to pressure drop is only valid when the moving water has a Reynolds number of 2,000 or less. If Re is higher than this, the water starts bouncing around unpredictably, and it takes more energy - more pressure - to shift it along.
As well as speed and pipe size, the Reynolds number Re depends on the ratio of the water's density to its viscosity, so to save having to work out (ρ/μ) each time you need to calculate Re I've included a table so that you can simply look it up.
| Temp oC | Viscosity μ | Density ρ | ρ/μ |
| 10 | 0.00133 | 999.7384 | 753,000 |
| 20 | 0.001 | 998.2 | 998,000 |
| 30 | 0.000753 | 996.6739 | 1,320,000 |
| 40 | 0.000567 | 995.1502 | 1,760,000 |
| 50 | 0.000427 | 993.6288 | 2,330,000 |
| 60 | 0.000321 | 992.1097 | 3,090,000 |
| 70 | 0.000242 | 990.5929 | 4,100,000 |
| 80 | 0.000182 | 989.0785 | 5,440,000 |
| 90 | 0.000137 | 987.5663 | 7,210,000 |
Example - Reynolds number
Cold water is flowing through a 15mm pipe run. How fast can it go before it starts to become turbulent?
The Reynolds number for this flow is
Re = (Speed) x (14/1000) x (753,000) = (Speed) x 10,500
(assuming "cold" means 10 deg.C and the pipe's internal diameter is 14mm), so if Re is to be 2,000 or less, then
Speed < 2,000/10,500 ... or Speed < 0.19 m/sec
Not very fast, then. How about hot water (at, say, 70 deg.C)?
Re = (Speed) x (14/1000) x (4,100,000) = (Speed) x 57,400
so Speed < 2,000/57,400 ... or Speed < 0.035 m/sec
which is really slow. Don't get too hung up on the numbers, by the way. Chaos is not exact. It's enough to say that turbulence is likely to start at around 0.2 metres/sec.
Is turbulent flow essential in domestic water systems?
Cold water flowing in 15mm pipe starts to become turbulent at the slow speed of 0.2 metres/sec. In 22mm pipe, the speed is lower still (0.13 m/sec). Does it matter that the water is moving so slowly?
The question is, how long are you prepared to wait for the sink or the bath to fill? A flow rate of 0.2 metres/second means that just 0.2m (20cm) of the pipe's contents come out of the tap in one second. Now, 22mm pipe (the size normally used to plumb in a bath) has an internal cross-sectional area of 320 sq.mm, so the volume occupied by 20cm of water is just:
Volume = Length x Area = (320 x10-6) x (20 x10-2) = 64 x10-6 cubic metres = 0.064 litres.
A bath holds typically 100 litres. It would take nearly half an hour to fill at this rate. Clearly 0.2 metres/second is far too low a speed to be useful. If a higher speed means turbulence, then so be it.
The trouble is that allowing turbulence is really not a good idea. For one thing, the particles of water are bashing into each other all the time, and that takes energy, and that means a much bigger force has to be applied to move it. For another, the force you need can't be calculated. It has to be inferred from other peoples' experiments.
Shake, rattle and moan
But the worst part of turbulence in pipes is the noise. In turbulent flow, particles of water move in random directions at random speeds. Well, so what? One particle of water is much like another. The problems begin when a particle decides, all by itself, to change into steam.
Large pressure differences can appear across very small volumes of turbulent water, especially when the water flows round a bend, or through a constriction like a valve or a tap.
In fact, bends can cause the flow to separate from the wall of the pipe, like this. Because the water is suddenly forced to move sideways across the pipe, whilst at the same time it is moving along the pipe, vortex eddies appear. They spiral off down the pipe, wasting energy as they go, until they are damped out by viscous friction. Bends should be avoided. If they are inevitable, then the more gradual they are, the better.
Sudden changes of velocity (that is, speed in a particular direction) cause equally sudden - and dramatic - local changes in pressure.
This creates problems because water at a lower pressure boils at a lower temperature. At the normal atmospheric pressure of 1 bar (14.5 psi, or 100,000 N/sq.m), water boils at 100oC of course, but if the pressure drops to 0.1 bar it will boil at only 47oC. The water in a central heating system is hotter than this.
When the local pressure somewhere in the water drops low enough, a particle of water turns immediately into a bubble of steam. The bubble soon moves back into a region of higher pressure and collapses, and the resulting shock wave zips through the water, bouncing off the pipe walls. The more turbulent the flow, the more often this happens. The process is known as cavitation, and it can corrode the pipework as well as a making a disturbing amount of noise. If you think about it, bubbles do form spontaneously in turbulent water. A waterfall, or the wake of a ship, or rocks in a stream all cause the water to foam. So does flushing the loo!
More speed means a lot more noise
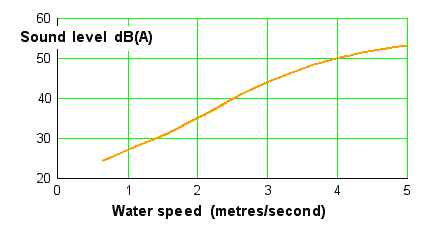
Measurements show that the cavitation noise from fittings (that is, elbows and tees) goes up with the speed the water is moving. Each increase of 1 m/s raises the noise level by a factor of about 4, and it's generally agreed that a water speed above about 3 metres per second makes cavitation noise unacceptably loud.
Cavitation isn't the only source of noise. Turbulence causes eddies to appear in the flow, and besides wasting energy they cause noise and vibration in the pipe network. Large eddies can be moving at up to 10% of the average speed of flow, and contain energy at frequencies from a minimum defined by
fmin = (Average water speed) / (Pipe diameter)
on upwards. For a 15mm pipe carrying water at 1.5 metres/sec, fmin turns out to be 100 Hz. Frequencies above 100 Hz contain progressively less energy, because viscous friction damps them more quickly.
The energy is coupled to the pipe network and may cause some part of it to resonate. The moving water acts rather like a white noise generator, seeking out any resonances in the pipe network. That's why pipes should be clamped firmly to the wall at intervals of no more than a metre or so. The speed of sound in water is about 1450 m/sec (at 15oC) - about 30% faster than in air - so a 1 metre length of pipe can't resonate at a frequency below about 700 Hz, and there shouldn't be enough stray energy there to worry about.
All this boils down to an engineering trade-off between cost and convenience. Slow-moving water implies large-diameter pipes, which would cost more to install. The key question is, how much noise will people accept?
Most sources recommend that the speed of water in pipes should be kept to less than 2 m/sec, and some specify a maximum speed of 1.5 or even 1 m/sec. Remember the Slug. The Reynolds numbers corresponding to usable water speeds for each size of pipe are summarised here.
| Re at... | 6 mm | 10 mm | 15 mm | 22 mm | 28 mm | 35 mm | 42 mm | 54 mm |
| 0.3 m/s | 2,600 | 4,800 | 7,300 | 11,000 | 14,000 | 18,000 | 21,000 | 28,000 |
| 1.0 m/s | 8,600 | 16,000 | 24,000 | 36,000 | 47,000 | 59,000 | 71,000 | 93,000 |
| 2.0 m/s | 17,000 | 32,000 | 49,000 | 73,000 | 94,000 | 120,000 | 140,000 | 190,000 |
The table shows clearly that the Reynolds number for water moving at 2 metres/sec is way larger than the 2,000-3,000 maximum that would guarantee non-turbulent flow. Real plumbing in real houses is designed on the basis that the water flow will be chaotic and turbulent. Unfortunately, there is as yet no proper theory to describe turbulent flow, so systems have to be designed on the basis of experience rather than physics. The simple theory I've been investigating just doesn't apply.
What happens in the real world?
So if there is no simple theory, is there a complicated one? Pipeline systems do get built, after all, and the engineers who design them must know what they're doing. How do they manage it?
Darcy-Weisbach
One key tool seems to be an expression called the Darcy-Weisbach equation, which predicts how much pressure would be needed to push a given fluid along a pipe at a particular speed. What makes it tricky to use is that it includes a "friction factor" ( f ) which depends not only on the smoothness of the pipe - since copper is smoother than, say, concrete, you'd expect it to have a smaller friction loss - but also the Reynolds number of the flow. But that in turn depends on the speed of flow. In other words, you can only calculate the speed if you already know the speed! It's not quite as daft as it sounds, but it's certainly rather complicated if you only want to design the plumbing in a house. I've included a worked example in part 2.
Real-world engineers prefer a simpler approach. They use the Hazen-Williams equation. The equation is strictly only valid for water at below about 25oC, but that's OK. It's much simpler than the alternatives. To use it, we need to know the head h, the pipe's length L and the 'hydraulic radius' (Rh - half the pipe's internal radius). And because the material the pipe is made from can also make a difference, there's a friction coefficient C which for ordinary copper or plastic pipe can be taken as 150. The graph below illustrates what the equation predicts will happen when the head is 3m, as it might be for a bath or shower. It shows that a small increase in the length of a short pipe makes a big difference to the flow-rate. On the other hand, you could safely add another 10m length to the garden hose without it making much difference at all.
Hazen-Williams
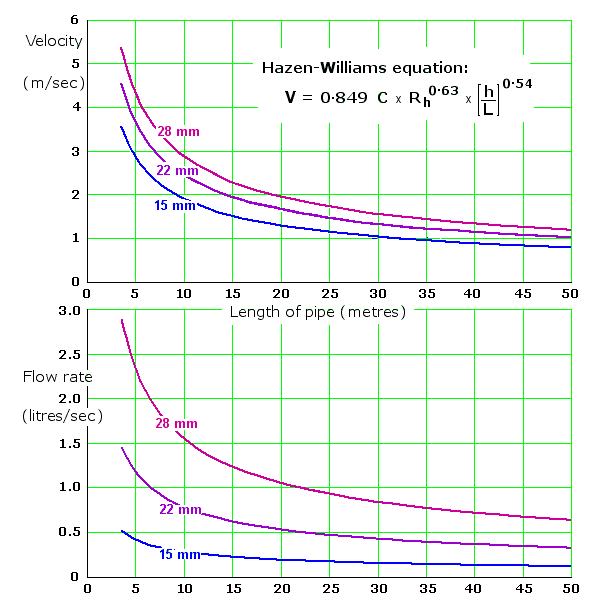
The graphs illustrate that the flow rate you can get from a given head drops off dramatically as the pipe length increases. But using the equation to design the plumbing in a house would lead to a lot of tedious calculation. There is a better and simpler approach, which I describe in part 2.
Real pipes for real houses
In the real world the range of pipe sizes you can actually buy is quite restricted. Builders' merchants usually stock the standard sizes listed in the table below. The size given (eg. 15 mm) is the outside diameter of the pipe.
Pipe dimensions
| Plumbers' merchants call it ... | 10 mm | 15 mm | 22 mm | 28 mm | 35 mm | 42 mm | 54 mm |
| Some plumbers know it as ... | 3/8 in | 1/2 in | 3/4 in | 1 in | 11/4 in | 11/2 in | 2 in |
| Internal diameter (mm) | 8.8 | 13.6 | 20.2 | 26.2 | 32.6 | 39.6 | 51.6 |
| Cross-sectional area (in mm2) | 61 | 145 | 320 | 539 | 835 | 1,232 | 2,091 |
In passing, it's worth pointing out that the standard sizes changed slightly when metrication was introduced. This might matter if the half-inch pipe that was installed in your kitchen thirty years ago is not exactly the same size as the new 15mm pipe you've just bought to plumb in the new dishwasher. The fittings may not quite, er, fit.
Smaller pipe must be cheaper and easier to install, so why isn't 10mm pipe used for everything? (In France, it often is!)
Small isn't always beautiful
A bath should fill in five minutes or so. Suppose in the interests of economy you decide to plumb it in with 10mm pipe. The bath holds about 100 litres, so to fill it in 300 seconds will require a flow rate of (100 / 300) = 0.33 litres/second. Now, the internal cross-sectional area of 10mm pipe is about 61 sq.mm, so a 1 metre length of it holds about 61 cubic millimetres, or 61 milli-litres (ml). A flow rate of 0.33 litres/sec therefore means a water speed of about (0.33 / 61 x10-3) = 5.4 metres/second - about 12 mph. Given enough pressure you probably could do it, but the roaring noise would frighten children and small animals, and cavitation damage would mean you'd have to replace the pipes and fittings after a few years anyway. It's probably a bad idea.
Each size of pipe is intended to carry a specific flow rate, quietly. Cross-sectional area is what matters here. A simple calculation of volumes shows that, at the maximum recommended water speed of 2 metres/second, the maximum flow rates are:
Maximum quiet flow rates
| 10 mm | 15 mm | 22 mm | 28 mm | 35 mm | 42 mm | 54 mm | |
| 1.5 m/sec | 0.08 | 0.22 | 0.45 | 0.82 | 1.3 | 1.9 | 3.1 |
| 2.0 m/sec | 0.1 | 0.3 | 0.6 | 1.1 | 1.7 | 2.5 | 4.2 |
To check the actual flow rate, get a bucket and a watch. A bucket usually holds 2 gallons ( = 16 pints, = 9.1 litres). At a 15mm pipe's maximum flow rate of 0.3 litres/sec, the bucket will fill in 30 seconds. At a 22mm pipe's maximum flow rate of 0.6 litres/sec, it will take 15 seconds.
Bath taps and sink taps
If 10mm pipe is not an option for the bath, then what is?
The idea is to choose the pipe sizes so that the water flows fast enough to fill the bath or the sink in a sensible time without making too much noise. A kitchen sink holds 10 or 12 litres of water. So to fill a 10 litre sink with water moving at 2 m/sec would take 85 seconds using 10mm pipe, 34 seconds with 15mm, 15 seconds with 22mm ... and just 2 seconds with 54mm pipe.
Now, if the sink filled in 2 seconds it wouldn't save much time on the washing up, and besides, water would splash all over the kitchen. Most people don't mind waiting half a minute or so for the sink to fill, and that's why kitchen sink taps are designed to be connected to 15mm pipe.
A bath holds about ten times as much as a sink: 100 to 120 litres. If both the hot and cold pipes are 22mm, and you run both at once, the flow rate is over 1.2 litres/second, so the bath fills in less than a minute and a half. Bath taps are designed for 22mm pipe.
If you want to know how to calculate real flow rates in a real system, the method is given here in Part 2.
Be warned - the numbers I use all refer to copper pipe. If you want to use plastic pipe you should be aware of the differences. You may find John Cantor's site interesting.