
This article shows how to calculate the amount of energy stored in a capacitor, and compares it with the energy stored in a similar-sized battery.
What's a capacitor?
Most capacitors consist of two parallel plates separated by an insulator. Sometimes the resulting sandwich is rolled up into a tube, like a Swiss roll, to save space, and some capacitors have multiple layers, like a club sandwich. I've written here about the concept of electric fields and capacitance, and illustrated what some real capacitors look like.
How can a capacitor store energy?
Left to themselves, a pair of positive electric charges want nothing to do with each other. They move apart as fast as they can. So if they are forced to move towards each other, they resist, and it takes energy to make this happen. The energy isn't used up and lost. It's stored, as an electric field - a kind of tension in space - for as long as the charges are held uncomfortably close together. When they become once again free to move, the charges use this energy to speed them on their way. A capacitor is a component specially designed to hold an electric field.
Explanation #1: Moving charges takes work
![]() Suppose you have a capacitor that has been charged to a voltage V, and you want to know how much energy it's currently storing. I showed here that the amount of energy (or Work, as some call it) needed to push a positive charge Q a bit closer to another one is the amount of charge moved, multiplied by the potential difference (that is, the voltage) that it has been pushed through.
Suppose you have a capacitor that has been charged to a voltage V, and you want to know how much energy it's currently storing. I showed here that the amount of energy (or Work, as some call it) needed to push a positive charge Q a bit closer to another one is the amount of charge moved, multiplied by the potential difference (that is, the voltage) that it has been pushed through.
![]() So common sense might suggest that a capacitor, charged to V, has required Q V joules of energy to reach that state, and so Q V joules is stored in the capacitor, ready to be used. Sadly, common sense is wrong, as usual. If you feel good after eating the first burger, will you feel twice as good when you finish the second?
So common sense might suggest that a capacitor, charged to V, has required Q V joules of energy to reach that state, and so Q V joules is stored in the capacitor, ready to be used. Sadly, common sense is wrong, as usual. If you feel good after eating the first burger, will you feel twice as good when you finish the second?
In fact, what happens is that, as the charges are forced closer and closer together, they resist more and more fiercely. It's not a linear process. Coulomb showed this with his inverse square law. The only way to do the sum is by integration. (Sorry. Life's like that sometimes.)
![]() To begin with, I assume that the capacitor C is holding a charge Q, which means I can measure a voltage V across it. Then if I apply a bit of energy δW to the system I can persuade a small amount of extra charge δQ to move onto the capacitor. So I can write an equation in terms of Q.
To begin with, I assume that the capacitor C is holding a charge Q, which means I can measure a voltage V across it. Then if I apply a bit of energy δW to the system I can persuade a small amount of extra charge δQ to move onto the capacitor. So I can write an equation in terms of Q.
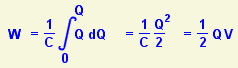 Then I can use integration to add up all the little δWs (and they're all slightly different) to discover how much energy was needed to move the total charge Q onto the capacitor. It turns out that the actual energy stored is exactly half what common sense predicted it would be.
Then I can use integration to add up all the little δWs (and they're all slightly different) to discover how much energy was needed to move the total charge Q onto the capacitor. It turns out that the actual energy stored is exactly half what common sense predicted it would be.
![]() In the real world, I don't usually know (or care) how much charge is stored, so it's more useful to write the stored energy in terms of the voltage and capacitance - both of which I can measure - like this:
In the real world, I don't usually know (or care) how much charge is stored, so it's more useful to write the stored energy in terms of the voltage and capacitance - both of which I can measure - like this:
Explanation #2: Keep the current constant
![]() There's another way of looking at this problem, by thinking about the current I (which I can easily measure, if I want to) rather than the charge Q (which I can't). Current is defined as the rate at which charge moves, so if I connect the capacitor to a constant-current power supply, charge Q will accumulate on the plates at a constant rate. The capacitor doesn't care how I charge it, but the sums become much easier.
There's another way of looking at this problem, by thinking about the current I (which I can easily measure, if I want to) rather than the charge Q (which I can't). Current is defined as the rate at which charge moves, so if I connect the capacitor to a constant-current power supply, charge Q will accumulate on the plates at a constant rate. The capacitor doesn't care how I charge it, but the sums become much easier.
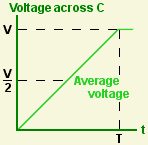
Suppose I take an uncharged capacitor and connect it across a power supply that delivers a constant current I. The voltage across the capacitor starts at zero and rises linearly until the component is fully charged. Then it stops. Call this maximum voltage V.
The average voltage across the capacitor whilst it's being charged is (V/2), so the average power being delivered to it is I (V/2). It was charged for T seconds, so the energy stored in the capacitor is T I (V/2).
![]() The charge accumulated on the capacitor is Q = I T, so the total energy stored is Q (V/2). This is the same result I got from integration. It's a nice illustration of the fact that it can be easier to solve a problem if you ask the right question in the first place.
The charge accumulated on the capacitor is Q = I T, so the total energy stored is Q (V/2). This is the same result I got from integration. It's a nice illustration of the fact that it can be easier to solve a problem if you ask the right question in the first place.
Joules compared to battery milliamp-hours (mAh)
Capacitors can store energy (in joules). So can batteries (but their energy is quoted in mAh). How do they compare? It should be possible to find out, since I know that 1 joule is 1 watt for 1 second.
Suppose I fully charge an electrolytic capacitor rated at 4,700μF 16v. It's about the size of a C cell - 50mm high and 25mm diameter, and so it could hold (0.5 x 4700x10-6 x 16 x 16) = 0.6 joules.
A typical rechargeable alkaline C size battery is rated at 1.2v, 2,200mAh, which seems to imply that it holds (1.2 x 2.2 x 60 x 60) = 9,500 joules. The battery can hold 15,000 times as much energy as the same sized capacitor! That's quite a difference! (And a non-rechargeable type has even more capacity.)
 However, I'm not really comparing like with like here. To begin with, the idea of battery 'capacity' is rather slippery. It depends on how you define it, and how you measure it.
However, I'm not really comparing like with like here. To begin with, the idea of battery 'capacity' is rather slippery. It depends on how you define it, and how you measure it.
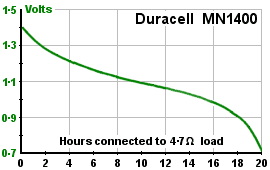
The Duracell MN1400 (a non-rechargeable alkaline C cell battery) has a nominal voltage of 1.5v and capacity of 7,000mAh. This implies it stores (1.5 x 7 x 60 x 60) = 38,000 joules. OK. I had a look at the published data. If you connect a 4.7Ω load across it, the voltage drops steadily with time. After 20 hours or so, the original 1.5v has fallen to 0.7v, and at that point you throw it away and buy another. If you calculate how much energy it's delivering to the load, hour by hour, and add them up, you get a total of about 19,000 joules - exactly half what you thought you were getting. The true capacity (at this load) is just 3.5Ah.

But with a less power-hungry load of 39Ω, not only does the battery last ten times longer, it now delivers over 30,000 joules, equivalent to 5,600mAh. A battery's 'capacity' depends on how quickly you want to get the energy out. My electrolytic capacitor, on the other hand, will happily give up all its energy in a millisecond, if that's what I need it to do.
I suppose that you could look at this the other way round, too. The rechargeable C cell I mentioned above (1.2v, 2.2Ah) holds 9,500 joules. A capacitor holding this much energy at 1.2v would have to be (2 x 9,500 / 1.2 x 1.2) = 13,000 Farads, so if it helps, you can think of a battery as an enormous capacitor.
Energy stored in a real capacitor - the earth!
And speaking of this, Professor Kraus reminds his readers in Electromagnetics, that "we live inside a huge capacitor" between the earth's surface and the 'electrosphere' - a conducting region of the upper atmosphere, around 25 km up, in which cosmic rays ionise the air molecules.
He calculates the earth's capacitance at about 0.18 Farad, which seems surprisingly low, and from the known value of charge density at the surface of the earth (around 3 nC/sq.m) he shows that this capacitor holds a million Coulombs or so. Then it's a simple matter to calculate how much energy it's storing. The figure he gets is 7,000,000,000,000 joules. That might seem huge, but it's roughly the amount of energy stored by the 300 million mobile phone batteries manufactured in China in a single year (2007).
Sources
Electromagnetics - John D. Kraus (McGraw Hill, 1991).
